在了解两个集合算子的并集和交集之间的区别之前,让我们首先了解集合论的概念。集合论是研究集合的数学的基本分支,特别是对象是属于还是不属于某种与某种数学相关的对象的集合。集合基本上是定义明确的对象的集合,这些对象可能具有或不具有数学相关性,例如数字或函数。集合中的对象称为元素,可以是数字,人,汽车,州等之类的东西。几乎所有东西和任何数量的元素都可以收集在一起以创建集合。
简单来说,集合是任意数量的无序元素的集合,这些元素可以看作一个整体。让我们了解集合的基本概念和表示法以及它的表示方式。这一切都始于对象x与集合A之间的二进制关系。为了表示x是否是集合A的成员,使用符号x ∊ A,而x∉A表示对象x不属于对象x。集合A。集合的成员列在花括号内。例如,小于10的素数集可以写为{2,3,5,7}。类似地,一组小于10的偶数可以写为{2,4,6,8}。假设地,几乎任何有限集都可以用其成员表示。
什么是集合联合?
两组A和B的并集定义为属于A或B或可能两者的元素集。它被简单地定义为所有不同元素或成员的集合,其中成员属于这些集合中的任何集合。并运算符对应于逻辑或,并由符号∪表示。它是包含两个集合的所有元素的最小集合。例如,如果集合A为{1、2、3、4、5},集合B为{3、4、6、7、9},则A和B的并集由A∪B表示并写入为{1、2、3、4、5、6、7、9}。由于数字3和4同时出现在集合A和B中,因此无需列出两次。显然,A和B的并集的元素数小于各个集合的总和,因为这两个集合中很少有相同的数字。
A = {1、3、5、7、9}
B = {3,6,9,12,15}
A∪B= {1、3、5、6、7、9、12、15}
什么是集的交集?
两个集合A和B的交集被定义为同时属于A和B的元素的集合。它简单地定义为包含集合A的所有元素(也属于集合B)的集合,以及类似的集B属于集A。相交运算符对应于逻辑与,并由符号represented表示。相反,两个集合的交集是包含两个集合共有的所有元素的最大集合。例如,如果集合A为{1、2、3、4、5},集合B为{3、4、6、7、9},则A和B的交集由A∩B表示并被写入如{3,4}。由于只有数字3和4在集合A和B中是相同的,因此将它们称为集合的交集。
A = {2,3,5,7,11}
B = {1、3、5、7、9、11}
A∩B= {3,5,7,11}
集的并集和相交之间的差异
- 基本-将两个集合A和B的并集定义为属于A或B或可能同时属于这两个元素的集合,而将两个集合的交集定义为同时属于A和B的元素集合。
- 符号表示–两个集合的并集由符号“∪”表示,而两个集合的交集由符号“∩”表示。
- 逻辑相关性–两组的并集对应于逻辑“或”,而两组的交集对应于逻辑“与”。
- 示例–令A = {a,e,i,o,u}并且
B = {a,b,c,d,e,f}
A∪B= {a,b,c,d,e,f,i,o,u}
A∩B= {a,e}
联合与交叉:比较表
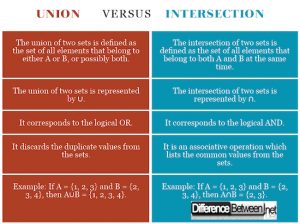
联合与交叉的摘要
并集和交集都是两个基本操作,可以通过这些基本操作对集合进行组合并使其相互关联。就集合论而言,联合是任何一个集合或两个集合中所有元素的集合,而交集是同时属于两个集合的所有不同元素的集合。两组A和B的并集符号为“A∪B”,而A和B的交集符号为“A∩B”。Set只是定义明确的对象(例如数字和函数)的集合,而集合中的对象称为元素。